この記事は会員限定です。会員登録（無料）すると全てご覧いただけます。
本連載では、第1回〜第3回で、ニューラルネットワークの仕組みと、TensorFlow 2.x（2.0以降）による基本的な実装コードを説明した。また、第4回〜第6回で、TensorFlow 2の書き方をまとめた。さらに前回（第7回）では「回帰問題」についてあらためて取り上げ、これまでの連載記事で学んできた知識だけでも「基本的なディープ ニューラル ネットワーク」（以下、DNN）の実装が十分かつ自由に行えることを体験していただいた。
これをもっと続けよう。あとは、ディープラーニングの実装パターンを繰り替えしながら、慣れていくだけである。数をこなせばこなすほど、最初は「難しい」「分からない」と思っていた部分はなくなっていく（最初は覚えることが多いが、覚えることが減っていけば、それだけディープラーニングが楽になり、より好きになるはずだ）。さっそく始めよう。
今回の内容と方針について
分類問題とは？
分類（classification）という用語は、一般的な意味と同じなので、説明は不要だろう。推論で出力された予測値により、事前に定義された複数の分類カテゴリー（＝機械学習では基本的に「クラス：class」と呼ぶ）の中のどれに最も該当するかを判別することである。
出力層の性質上、ニューラルネットワークの分類問題は、下記の2つに大別される。
- 二値分類（Binary classification）
- 多クラス分類（Multi-class classification）
二値分類
第1回〜第3回でも、座標点の色が「オレンジ色（-1.0）か」「青色（1.0）か」を分類するニューラルネットワークについて説明してきた。このような分類を二値分類と呼ぶのである。ただし、
- 「-1.0か」「1.0か」
という数値は実は扱いにくい。連載初回の3回は「ニューラルネットワーク Playground - Deep Insider」の挙動にサンプルコードを完全一致させることで、理解がスムーズになるよう、-1.0／1.0という数値範囲にしたが、これは一般的ではない。
通常のニューラルネットワークでは、
- 「0か」「1か」
の二値で分類を判断する。例えば、今述べたオレンジ色を-1.0ではなく0で、青色を上と同じく1で表現したとすると、0（推論の結果、オレンジ色である確率）が80％のとき、1（青色である確率）は20％である。また、0が0％のとき、1は100％となる。つまりこの「0か」「1か」は1つの値にまとめられる（一方の値を「x％」とすれば、もう一方の値は「（100-x）％」と表現できる）。よって二値分類では、出力層には1つの「ニューロン」（第2回で説明したように、場面に応じて「ユニット」や「ノード」とも呼ばれる）を用意すればよい。
「0か」「1か」（つまり合計100％）にするには、出力層のニューロンが出力する値を0.0〜1.0の範囲に収める必要がある。この処理を一般的にはシグモイド関数（Sigmoid function）という活性化関数によって実現する（図1）。ちなみに、合計100％にするのは人間が分かりやすいからだ。-1.0〜1.0だと合計200％となってしまい、例えば
- 「-1が132％で、1が68％」
と言われても直感的にピンと来ないのではないだろうか。一般的な人間にとっては「普通に100％確率値で言ってよ」となるだろう。
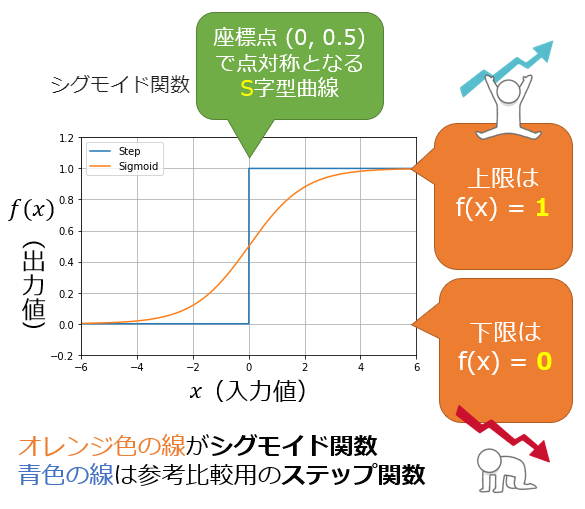図1 シグモイド関数の出力は0〜1に変換される二値分類のために、活性化関数としてシグモイド関数を使った場合、セットで使われる損失関数が基本的に決まっており、具体的には二値分類用の交差エントロピー（Binary Cross Entropy）が使われる（※ちなみに交差エントロピーは、日本語では「クロスエントロピー誤差」と表記されることがあり、英語では「Cross Entropy Loss」と表記されることが多いので注意してほしい）。「二値分類用」と書いたのは「多クラス分類用」もあるからである。次にその多クラス分類について説明しよう。
多クラス分類
「0か」「1か」だけでなく、「2か」「3か」〜「9か」と、多数の分類カテゴリー（＝クラス）があるようなケースを、多クラス分類と呼ぶ。これまで連載記事では取り扱っていないので、今回はこの多クラス分類が主題となる。この、
- 「0」「1」〜「9」
といった0スタートの番号は、クラスインデックス（class index）と呼ばれる（ライブラリによってはスパースラベル：sparse labelsと記載されていることもある）。ちなみに0スタートであることは、配列インデックスと一致するので、プログラミングしやすいというメリットもある。
クラスインデックスは、主にカテゴリー変数（categorical variable、カテゴリカル変数）に割り当てられる。例えば「猫」「虎」「ライオン」というカテゴリー変数がある場合、
- 「猫＝0」「虎＝1」「ライオン＝2」
といったように割り当てられる。このような割り当てを、カテゴリー変数エンコーディング（Categorical variable encoding）と呼び、特にクラスインデックスにエンコーディングする手法は数値エンコーディング（integer encoding）などと呼ばれる。
少し脱線するが関連情報として、数値エンコーディング以外で特に有名なのが「ワン ホット エンコーディング」（one-hot encoding）である。これは、カテゴリー数分の変数（数学的には「ベクトル」、プログラミング的には「配列」）を用意しておき、そのうちの1つだけが1で、それ以外は0になるようにエンコーディングする手法である。例えば10個のカテゴリー（例：猫、虎、……、ピューマ）があり、対応するカテゴリー変数がクラスインデックス（例：猫＝0、虎＝1、〜、ピューマ＝9）となっている場合に、10個の変数を用意し、例えば、その10個目（＝クラスインデックスは9）の変数のみが1で、それ以外は0になるようにする。つまり、
- 「クラスインデックス＝9」
という1つの変数が、
- 「0、0、0、0、0、0、0、0、0、1」
という10個の変数（one-hotベクトルやone-hot表現と呼ばれる）に展開されるわけである。one-hotエンコーディングは、多クラス分類を行う際に直感的で便利ではあるが、上記のように特殊なエンコーディングを行う必要性が発生するというデメリットもある。そこで本稿ではクラスインデックスを用いる。
クラスインデックスを使うにしろ、one-hot表現された複数変数を使うにしろ、先ほどの二値分類とは異なり、出力層のニューロンが1つというわけにはいかない。例えば「猫」「虎」「ライオン」……と3つ以上あるのであれば、出力層もそれぞれに対応する3つ以上のニューロンが必要になる。
なお、二値分類の場合と同様に、出力層のニューロンが出力する値は100％確率値で表現した方が分かりやすい。例えば、
- 出力値の例1： 「猫＝3.2」「虎＝1.2」「ライオン＝0.3」
- 出力値の例2： 「猫＝10.2」「虎＝5.2」「ライオン＝0.6」
という予測結果値が出力されるよりも、
- 出力値の例1： 「猫＝68.1％」「虎＝25.5％」「ライオン＝6.4％」
- 出力値の例2： 「猫＝63.7％」「虎＝32.5％」「ライオン＝3.8％」
というような100％確率値で表現された方が、理解や（例1と例2などで）比較がしやすいだろう。
このように多クラスを合計100％にする活性化関数が、ソフトマックス関数（Softmax function）である。図2は「虎（Tiger）＝緑色の線」に1.0、「ライオン（Lion）＝赤色の線」に0.0という固定値を入力し、「猫（Cat）＝オレンジ色の線」をX軸に取り-6.0〜6.0で変化させたときのグラフである。X軸上のどこを取っても、3つの値の合計は1.0（つまり100％）となる。
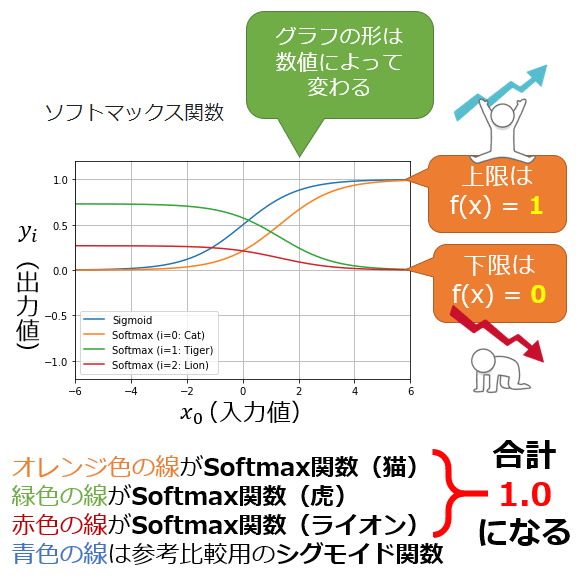図2 ソフトマックス関数が出力する予測値の合計は100％になる図中のiはクラスインデックスを意味するので、猫（i＝0）／虎（i＝1）／ライオン（i＝2）となる。
x0は、入力値（x）が「猫（i＝0）」であることを指す。
yiは、猫（i＝0）／虎（i＝1）／ライオン（i＝2）それぞれの入力値に対する、ソフトマックス関数の出力値（y）を意味する。
ソフトマックス関数により例えば、
- 「猫＝0.0」「虎＝1.0」「ライオン＝0.0」なら
→ 「猫＝21.2％」「虎＝57.6％」「ライオン＝21.2％」（図2のx軸が0のところを参照） - 「猫＝-0.5、虎＝1.0、ライオン＝0.0」なら
→ 「猫＝14.0％、虎＝62.9％、ライオン＝23.1％」 - 「猫＝4.0、虎＝1.0、ライオン＝0.0」なら
→ 「猫＝93.6％、虎＝4.7％、ライオン＝1.7％」
というように予測値が確率値に変換される。いずれも合計すると100％になる。
多クラス分類のために、活性化関数としてソフトマックス関数を使った場合も、セットで使われる損失関数は基本的に決まっている。具体的には多クラス分類用の交差エントロピー（Categorical Cross Entropy）である。二値分類用とは計算方法が異なるが、要するに分類では基本的に「交差エントロピーを使う」ということである。なお、交差エントロピーの中身の計算式を知っておくに越したことはないが、知らなくても実用上の問題は基本的にないので、本稿では説明を割愛する。
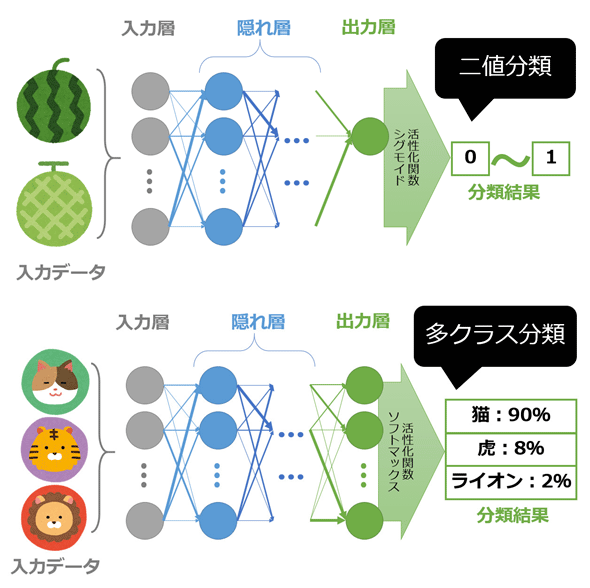
二値分類と多クラス分類の出力層の比較
以上、ニューラルネットワークで表現できる2つの分類方法を紹介した。簡単に図3にまとめておこう。
図3 二値分類と多クラス分類でのニューラルネットワークの比較今回、取り扱う分類問題について
今回の記事で一番重要な部分は、ここまでに説明してきた内容である。あとは、いつものワンパターンのコードをちょこちょこっと書き換えて実装していくことになる。強いて本稿のもう一つのポイントを挙げるなら、過学習の体験である。そこに注目して読み進めてほしい。
分類問題として、本稿では最初に多クラス分類を取り扱う。そこで使用するデータは、「Fashion-MNIST」というファッション商品（写真）の画像データセットである（詳細後述）。必要な箇所にはしっかりと解説を入れている。
次に、二値分類を取り扱う。そこで使用するデータは、「MNIST」という手書き数字の画像データセットである（そのうちの「0」と「1」の手書き数字だけを使用する。詳細後述）。こちらは、多クラス分類とほぼ同じようなコードとなっており、活性化関数や損失関数などを少し書き換えるだけである。よって、コードの変更箇所を簡単に示すだけで詳しくは解説しない。
おまけとして二値分類の最後では、実運用をイメージし、Web上で「0」か「1」の数字を読者自身が手書き入力をして、その画像を「0」か「1」かに分類する実例（Webアプリ）を説明している。ここまで試すことで、ディープラーニングの実用に現実感が持てるだろう。
図4 ディープラーニングの実運用イメージ（Webアプリ）今回、採用するTensorFlow 2の書き方について
前回に引き続き、サブクラスモデル（Subclassing API）で実装する。学習／トレーニングでは、compile()＆fit()メソッドを利用することとする。
本稿で説明する大まかな流れ
基本的な実装の流れはワンパターンで、具体的には以下の通りだ。
- （0）本ノートブックを実行するための事前準備
- （1）データの準備
- （2）モデルの定義
- （3）学習／最適化（オプティマイザ）
- （4）評価／精度検証
- （5）テスト／未知データによる評価
- 実運用のイメージ
―――【二値分類編】―――（※上記と同様の手順から変更箇所のみ説明）
- （6）データの準備
- （7）モデルの定義
- （8）学習／最適化（オプティマイザ）
- （9）評価／精度検証
- （10）テスト／未知データによる評価
- 実運用のイメージ
それでは、実際にTensorFlow 2を使って、この分類問題を基本的なDNNだけで解いてみよう。
（0）本ノートブックを実行するための事前準備
前提条件
今回は、Python（バージョン3.6）と、ディープラーニングのライブラリ「TensorFlow」の最新版2.2を利用する。また、開発環境にGoogle Colaboratory（以下、Colab）を用いる。
前提条件の準備は第1回など、これまでと同じなので、説明を省略する。詳しくはColabのノートブックを確認してほしい。
次のページは……
前置きが少し長くなったが、いよいよ実践だ。次のページで多クラス分類を実装してみよう。
Copyright© Digital Advantage Corp. All Rights Reserved.
"一般的な" - Google ニュース
June 08, 2020 at 03:00AM
https://ift.tt/2MAAqjJ
第8回 分類問題をディープラーニング（基本のDNN）で解こう - @IT
"一般的な" - Google ニュース
https://ift.tt/2Raf92k
Shoes Man Tutorial
Pos News Update
Meme Update
Korean Entertainment News
Japan News Update
Bagikan Berita Ini
0 Response to "第8回 分類問題をディープラーニング（基本のDNN）で解こう - @IT"
Post a Comment