実践的基礎知識役に立つ平均編（2）＜算術平均と幾何平均＞ | 富裕層向け資産防衛メディア - 幻冬舎ゴールドオンライン

ピクテ投信投資顧問株式会社が、実践的な投資の基礎知識を初心者にもわかりやすく解説します。※本連載は、ピクテ投信投資顧問株式会社が提供するコラムを転載したものです。

算術平均と幾何平均

算術平均と幾何平均は、それぞれに特徴があってどちらが優れているということではなく、大切なことは両者の特徴を知り、意味するところを知ることです。算術平均とは一般的によく使われている平均で、対象となる全データを合計してデータの個数で割ることで求められます。また、幾何平均とは累積結果に至るまで平均してどのくらいのペースで変化していったのかを表すもので、平均収益率や平均成長率などを考える上で役に立ちます。

幾何平均

前回のレポートで、「幾何平均(相乗平均)」は平均収益率や平均成長率、平均変化率を考える上で役に立つと紹介させていただきましたが、一般的な算術平均(相加平均)とどう違うのでしょうか。

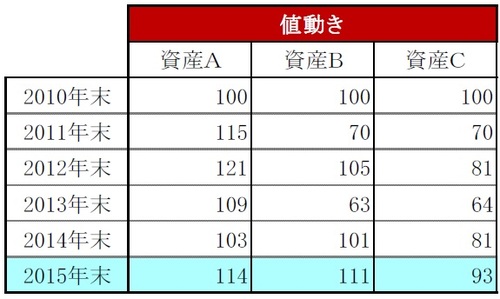
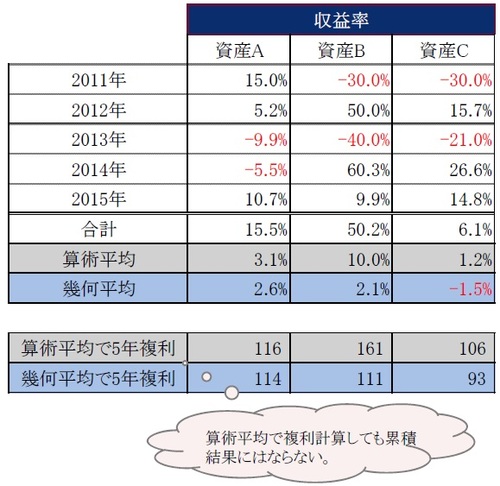
たとえば、図表1のような値動きをした資産A、B、Cがあったとします。各資産の各年の収益率を計算すると図表2のようになります(それぞれ図表1、2参照)。

［図表1］各資産の値動き

［図表2］各資産の収益率 ※数値は四捨五入して表示しているため、表示されている数値での計算結果と不一致となる場合があります。

資産Aの収益率の算術平均は

(15.0%+5.2%-9.9%-5.5%+10.7%)÷5=3.1%

と3.1%になります。

もし、この算術平均の3.1%で5年間複利運用をすると

100×(1+0.03)5=116

となり、100は116まで増えることになります。この116は2015年末の114という値と一致しません(図表2参照)。

一方、資産Aの収益率の幾何平均は

5√{(1+15%)×(1+5.2%)×(1-9.9%)×(1-5.5%)×(1+10.7%)}-1=2.6%

と2.6%になります。

この幾何平均の2.6%で5年間複利運用をすると

100×(1+0.026)5=114 

となり、2015年末の114と一致します。

実は、これはごく当たり前のことで、算術平均というのは相加平均という言葉が示すように、各数字を加算、つまり足して計算するため、算術平均を5回足し合わせれば各収益率の合計に一致しますが、複利計算をしても累積結果にはなりません。

幾何平均は相乗平均という言葉が示すように各数字を乗算、つまり掛けて計算するため、足しても各収益率の合計にはなりませんが、複利計算すれば累積結果と一致します。

このように、各年の平均収益率や平均成長率、平均変化率のような、「それまでの結果から何%変化したか」を集計したものを使って、累積結果に至るまでに平均してどのくらいのペースで変化していったのかを考えるうえで、幾何平均は役立ちます。

当レポートの閲覧に当たっては【ご注意】をご参照ください（見当たらない場合は関連記事『実践的基礎知識役に立つ平均編（2）＜算術平均と幾何平均＞』を参照）。

Let's block ads! (Why?)

"一般的な" - Google ニュース
February 15, 2020 at 03:05AM
https://ift.tt/39zCOAN

実践的基礎知識役に立つ平均編（2）＜算術平均と幾何平均＞ | 富裕層向け資産防衛メディア - 幻冬舎ゴールドオンライン
"一般的な" - Google ニュース
https://ift.tt/2Raf92k
Shoes Man Tutorial
Pos News Update
Meme Update
Korean Entertainment News
Japan News Update

Bagikan Berita Ini